Why is Only a 3-Phase Power Supply System Used Instead of 2-Φ, 4-Φ, 6-Φ, 12-Φ, or More Phases for Power Transmission and Distribution?
Are you wonder Why 3-Phase Power? Why Not 6, 12 or More for Power Transmission? The most common power supply systems used in transmission, distribution, and utilization are the Single-Phase and Three-Phase systems. The Three-Phase power system offers several advantages over the Single-Phase system, especially for transmitting large amounts of power efficiently and economically. For example, a three-phase motor runs more smoothly and delivers constant torque compared to a single-phase motor, which has noticeable pulsations.
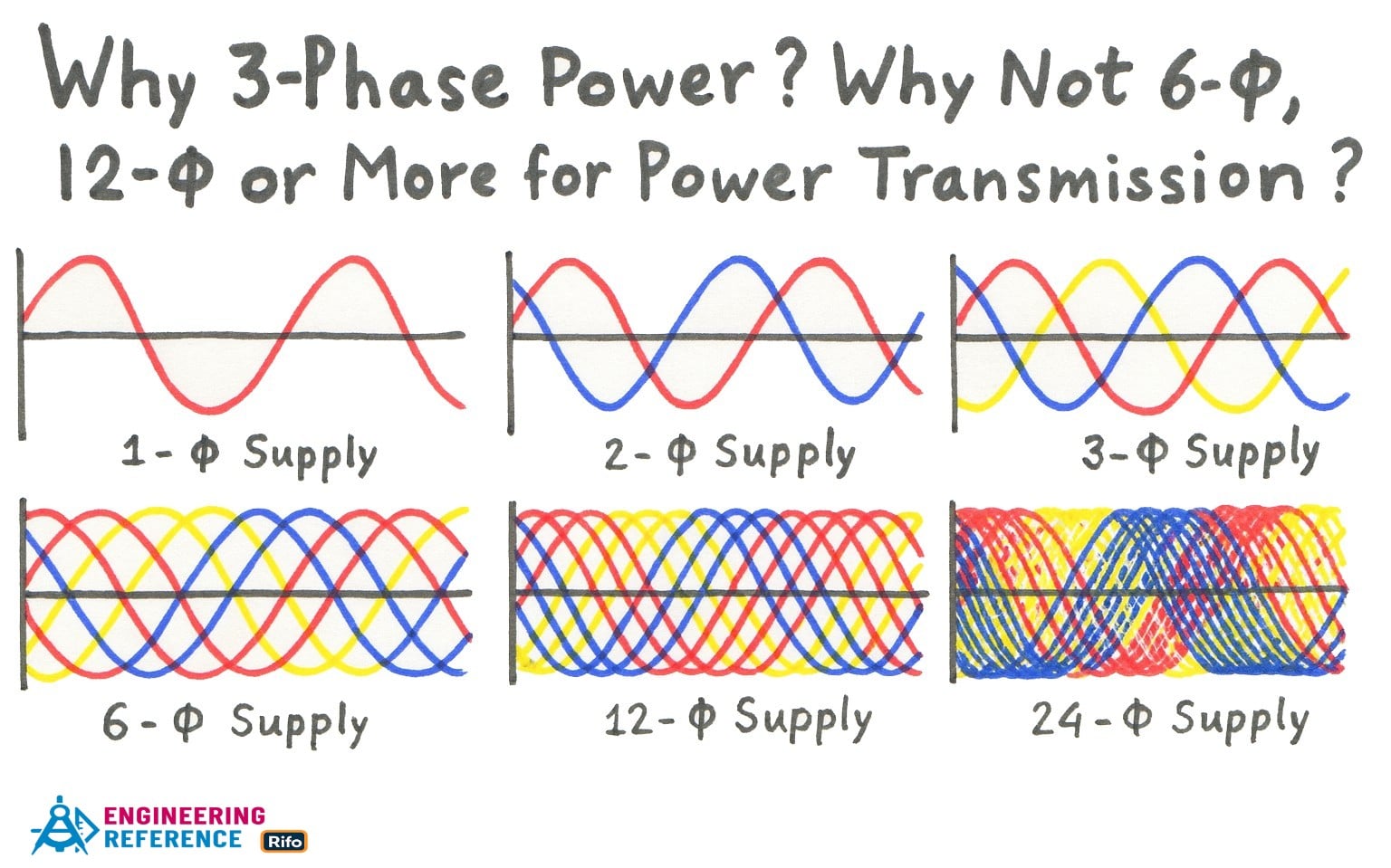
It’s important to note that systems with more than three phases—such as 6-phase, 9-phase, or 12-phase—are indeed used in power electronics applications like rectifier circuits and Variable Frequency Drives (VFDs). These systems help reduce ripple and produce smoother DC output. Think of it like using more lanes on a highway to make the traffic (current flow) smoother and more stable.
Although it is technically possible to create a multi-phase system using phase shifting transformers or a motor-generator set, doing so for power transmission and distribution is not practical. These methods are more complex, expensive, and less efficient for large-scale systems. That’s why the 3-phase system has become the standard—it provides the best balance between simplicity, efficiency, and cost for long-distance power transmission and distribution.
Read More : Why is a Battery Rated in Ah (Ampere hour), Not in VA?
Why 3-Phase Instead of 1-Phase Supply System?
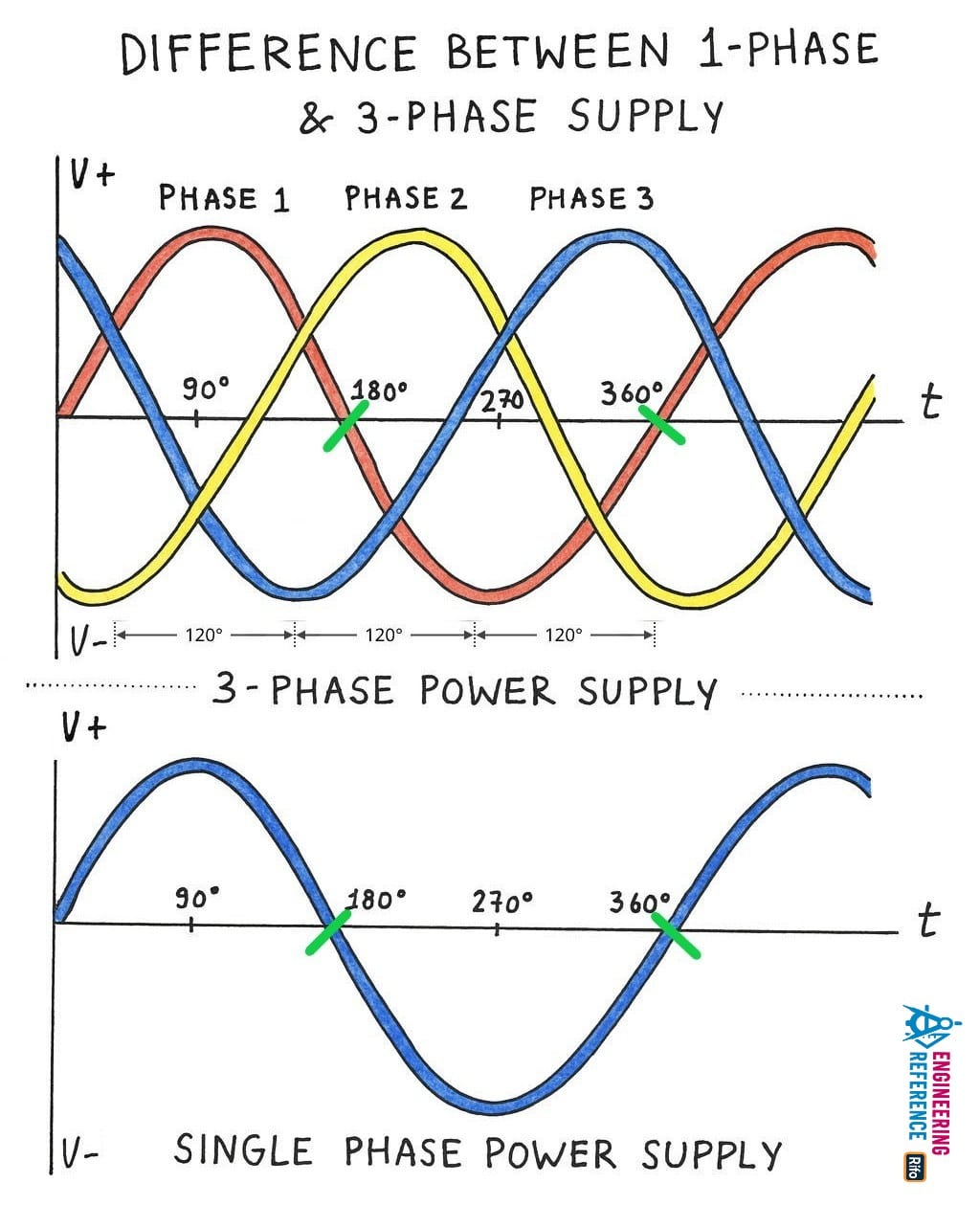
The main reason for using a three-phase system instead of a single-phase or two-phase system is that it can deliver more constant and uniform power. In simple terms, a three-phase supply transmits electricity more smoothly and efficiently, making it ideal for industrial and large-scale applications.
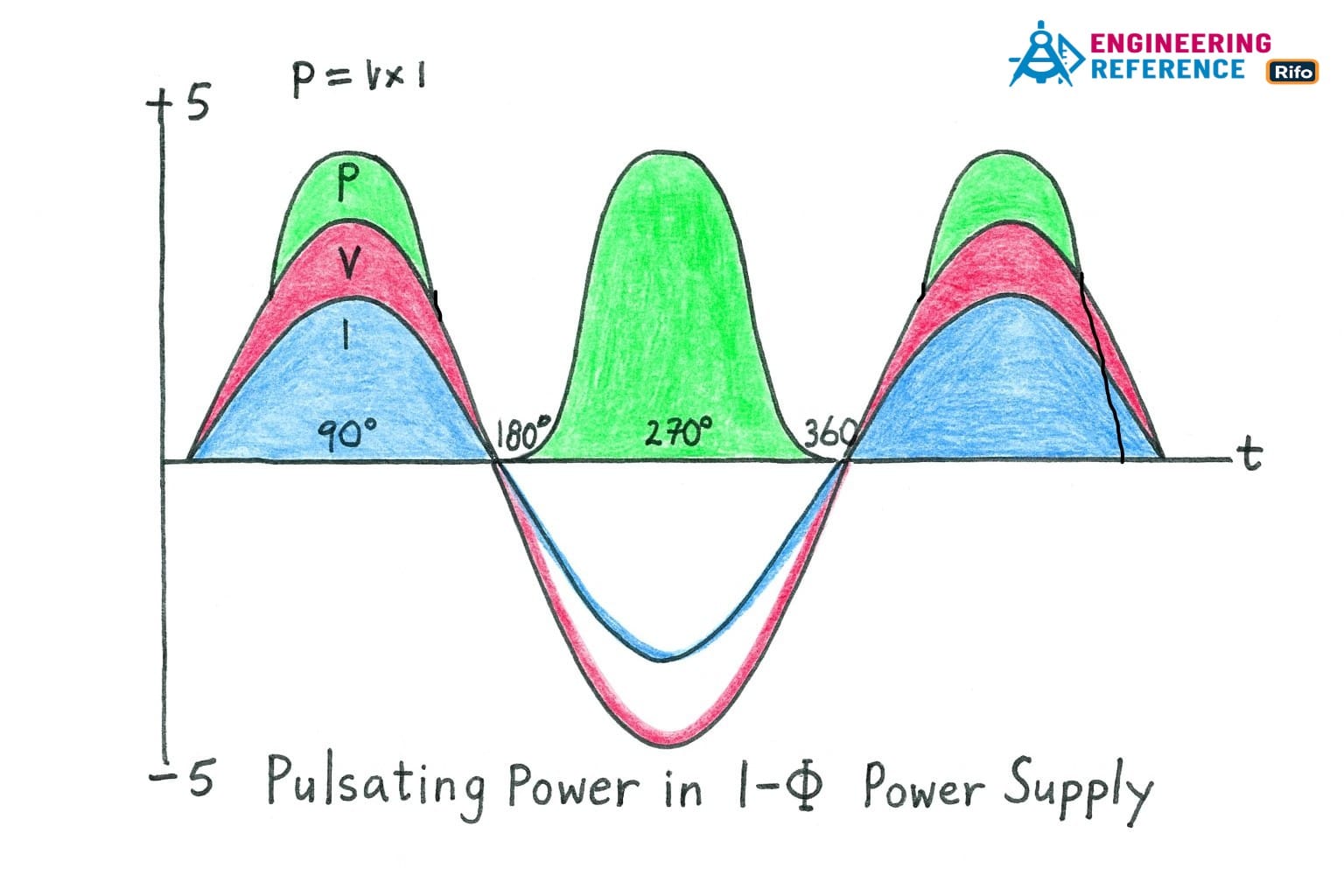
Power in a Single-Phase System
P = V . I . CosΦ
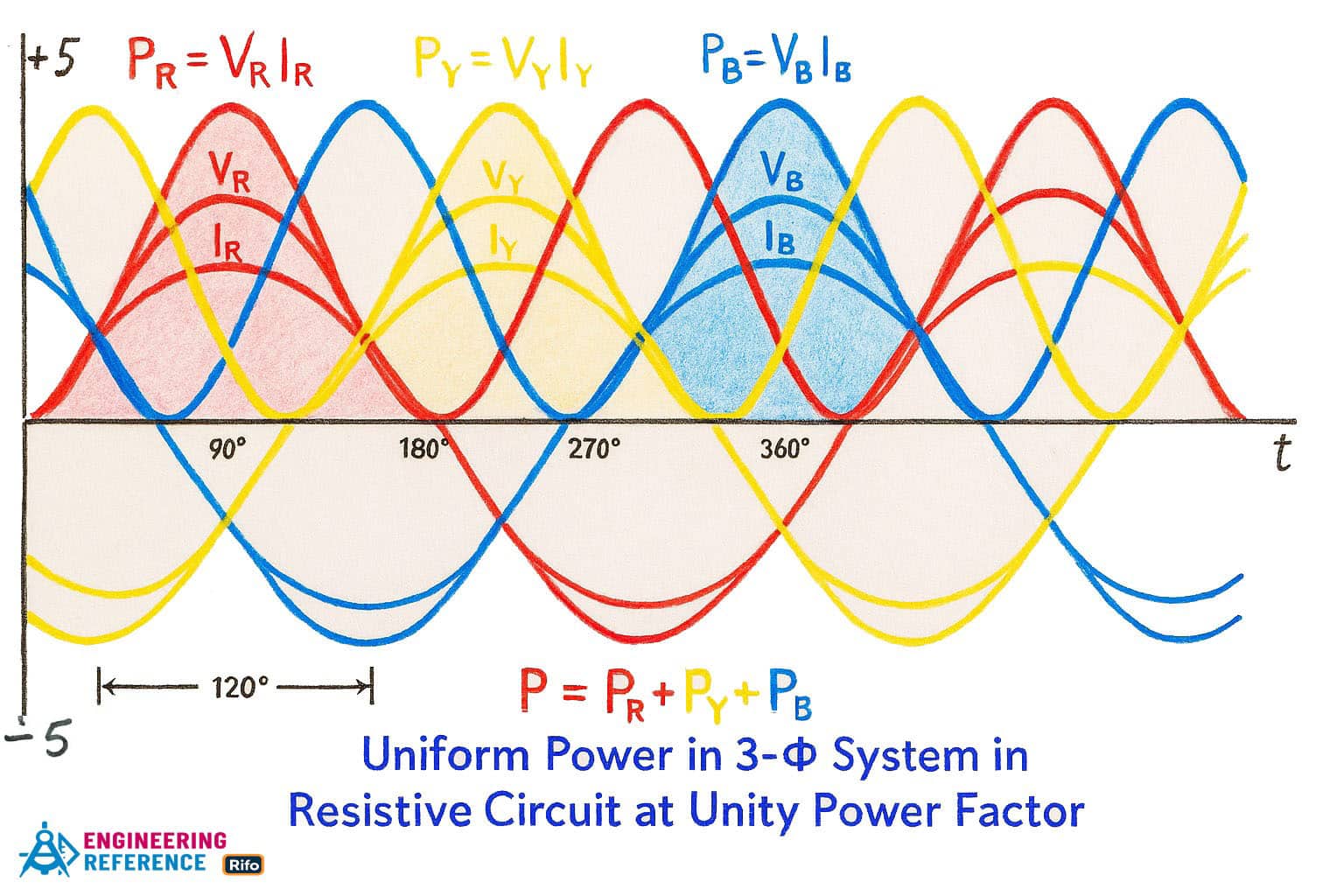
Power in a Three-Phase System
P = √3 . VL . IL . CosΦ … or
P = 3 × VPH . IPH . CosΦ
Where:
P = Power in watts
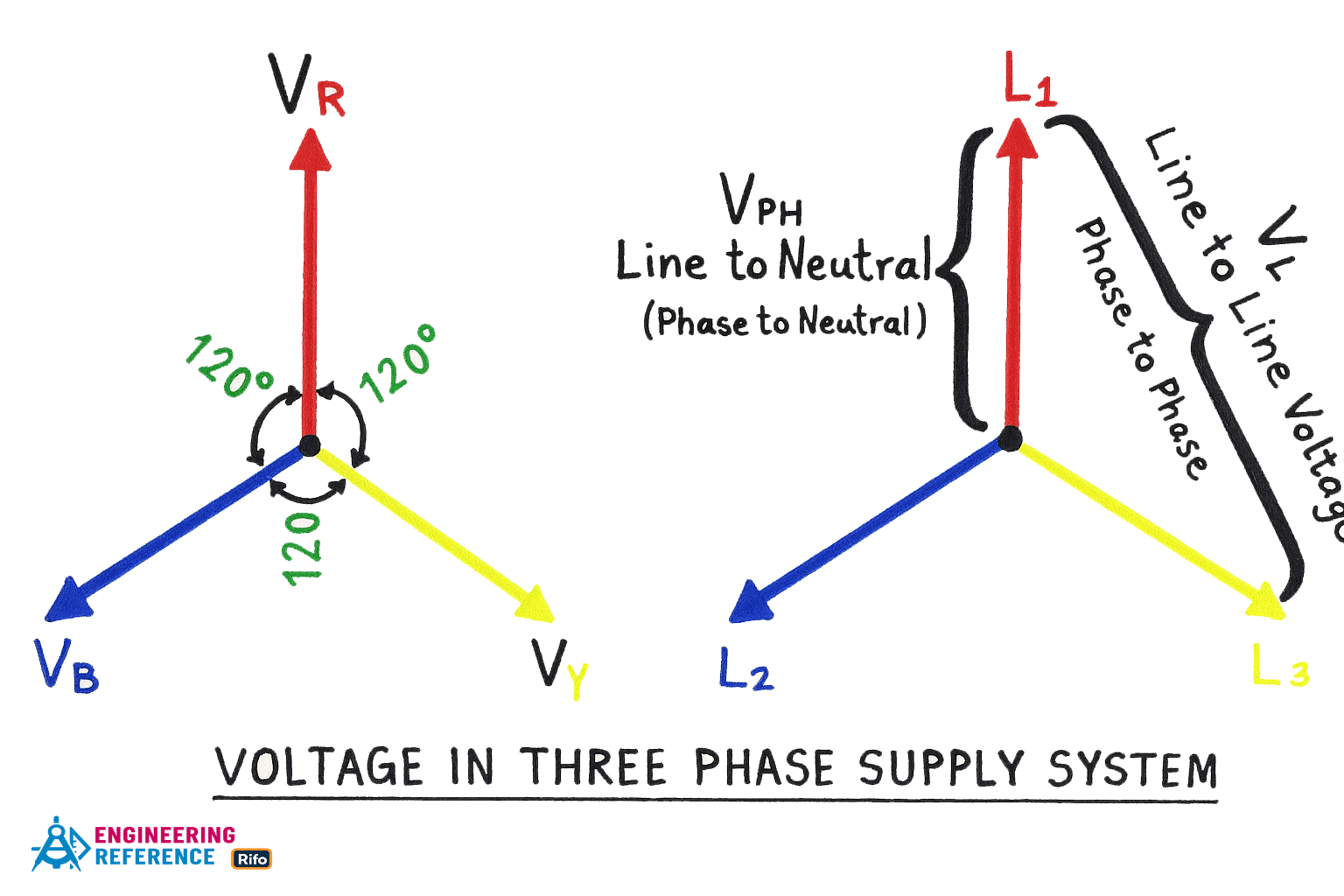
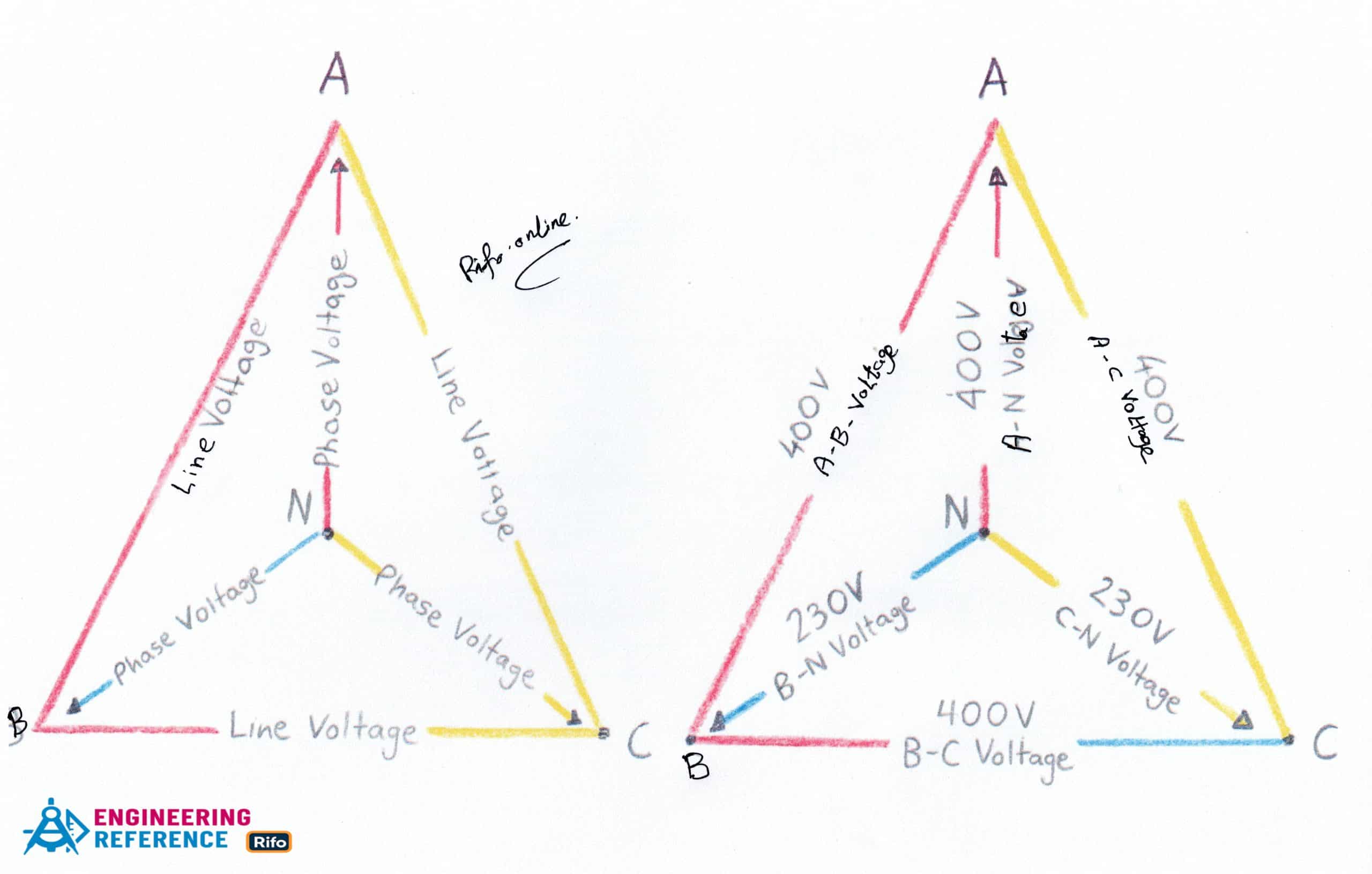
VL = Line voltage
IL = Line current
VPH = Phase voltage
IPH = Phase current
CosΦ = Power factor
From these formulas, we can see that a three-phase system can deliver 1.732 times (√3) more power than a single-phase system. In comparison, a two-phase system can transmit about 1.141 times more power than a single-phase system.
Another major advantage of a 3-phase supply is the presence of a Rotating Magnetic Field (RMF). This RMF allows three-phase motors to start by themselves and run with constant torque and power output. In contrast, a single-phase supply does not produce an RMF, resulting in pulsating power and motors that need an external starter. You can think of it like riding a bike—three-phase power gives a smooth, steady push on every pedal stroke, while single-phase power feels like pedaling unevenly with pauses in between.
The 3-phase system also experiences less voltage drop and lower transmission losses than the single-phase system. For instance, in a typical resistive circuit:
Single-Phase System
Power loss in the line = 18I²r (P = I²R)
Voltage drop in the line = I.6r (V = IR)
Three-Phase System
Power loss in the line = 9I²r (P = I²R)
Voltage drop in the line = I.3r (V = IR)
This clearly shows about a 50% reduction in both power loss and voltage drop when using a three-phase system compared to a single-phase system.
Learn more about : Why is a Transformer Rated in kVA, and Not in kW?
Now, while a two-phase system also produces an RMF and constant torque, the three-phase system still transmits more power because of its additional phase. This raises the question—if more phases mean more power, why not use 6, 9, 12, or even 24 phases? We’ll explore this in detail and explain why the three-phase system offers the best balance of efficiency, simplicity, and economy for power transmission and distribution.
Good to Know
In a three-phase system, each phase is separated by a 120° phase angle. This means that the three alternating currents reach their peak values at evenly spaced times, keeping the total power flow smooth and constant.
In contrast, a two-phase system has a 90° phase difference between its two voltages. This smaller separation causes less uniform power delivery compared to the three-phase system. You can imagine it like three people taking turns pushing a swing at perfect intervals (120° apart) — the swing moves steadily. But if only two people push at 90° intervals, the swing’s motion becomes uneven.
Why Not 6-Φ, 9-Φ, or 12-Φ Instead of 3-Φ?
It might seem logical to think that if increasing the number of phases gives smoother power and less loss, then using 6-phase, 9-phase, or 12-phase systems would be even better. Indeed, polyphase systems provide Rotating Magnetic Fields (RMF), constant torque, and uniform power output, and adding extra phases can further reduce transmission losses and voltage drops. So, why do we still use only the 3-phase system for power transmission and distribution?
The answer lies in efficiency, simplicity, and cost. Among all polyphase options, the 3-phase system is the smallest configuration that provides smooth and balanced power with the least number of conductors—only three wires, compared to twelve wires in a 12-phase system. Despite using fewer conductors, the 3-phase system delivers nearly the same practical performance.
Another key reason is the 120° phase angle separation between the three phases. This specific spacing perfectly cancels out the third harmonic and its multiples, which greatly improves power quality. Systems with 6, 9, or 12 phases do not eliminate these harmonics as effectively and introduce unnecessary complexity.
Using more phases would also make the entire power network more complicated and expensive. For example, a 12-phase system would require 12 conductors, larger busbars, more circuit breakers, transformers (T/F), current transformers (CTs), potential transformers (PTs), and additional protective equipment. It would also increase the height and size of transmission towers, take up more substation space, and demand higher maintenance costs.
In short, the 3-phase system offers the best balance between performance, economy, and simplicity. It provides smooth, reliable power transmission without the unnecessary cost and complexity of higher-phase systems. That’s why it remains the universal standard for generation, transmission, and distribution of electrical power.
Explore engineering concepts in : Why are there Grooved Slots in the Pins of Two Pin Plugs?
Why Not 2-Phase? Why Only 3-Phase?
If both 2-phase and 3-phase systems can produce a Rotating Magnetic Field (RMF), constant torque, and steady power, then why is the 3-phase system preferred? The main reason is that the extra phase in a 3-phase supply allows it to transmit more power with the same number of conductors and overall greater efficiency than a 2-phase system.
In a 2-phase system, four wires are usually required to carry power from the generator to the load — each phase has its own line and neutral to complete the circuit. To reduce the number of wires, engineers can use a common neutral, turning it into a 2-phase, 3-wire system. However, this setup causes a problem: the neutral conductor must handle the combined return current from both phases, which is much higher. As a result, a thicker neutral wire (often copper) is needed, increasing material costs.
The 3-phase system, on the other hand, solves this issue naturally. With only three conductors (one for each phase), it delivers higher power output and maintains balanced load conditions without requiring an oversized neutral wire. In a balanced or symmetrical load, or when connected in a delta configuration, only three wires are needed. For unbalanced or asymmetrical loads, a fourth wire (neutral) is added in a star configuration to ensure smooth operation and voltage stability.
Therefore, the 3-phase power system provides the ideal combination of efficiency, balance, and cost-effectiveness. It offers all the benefits of a 2-phase system—like RMF and constant torque—while eliminating its wiring and current-return disadvantages, making it the standard choice for power transmission and distribution worldwide.







